Hyperparameter Tuning
Introduction
Many machine learning algorithms come with a set of hyperparameters – parameters which are not optimised during the actual learning step. Tuning these hyperparameters improves the model’s predictive power and constitutes an integral part of model learning.
This article briefly addresses the task of hyperparameter tuning. It then shows how to perform the tuning with R and gives an example for improving the random forest based trading strategy presented in an earlier article.
Hyperparameters in Machine Learning
While a machine learning algorithm’s parameters can be learned from the data provided, hyperparameters are external to the task in the sense that they cannot be learned from data. Instead, for each set of hyperparameter values the learning algorithm might behave slightly different. By fine-tuning hyperparameters, often the predictive power of a model can be increased. Manual tuning can be performed by altering the hyperparameter values and examining the change in the model’s generalization error, which for example could be evaluated through cross-validation. Mathematically speaking, hyperparameter tuning is an optimization problem. As for each set of hyperparameter values the actual learning itself is often very costly, searching the entire feasible hyperparameter space is often not possible. The example in the next section comes with a discrete hyperparameter search space – which is why brute forcing the optimal hyperparameter set in that case is practicable.
The following list gives some examples for machine learning algorithms and some of their hyperparameters:
- Random Forest: Number of trees, bag size, number of variables for splits, tree depth, splitting rule
- Neural network: learning rate, loss function, batch size, number of epochs, regularisation parameter
- K-nearest-neighbor: K
- Regularised regression: regularisation parameter
Application to Random Forest Trading Strategy
Hyperparameter tuning can be used to improve performance of the trading strategy presented in an earlier article. The following two articles provide the relevant background details and implementation:
The following R scripts will require the dataframesdf_training and df_test to exist in the R workspace. Both dataframes are constructed in the trading strategy article. As the strategy is based on a learned random forest it is possible to tune its parameters “number of split variables”, “number of trees” and “minimum node size”. Tuning can be achieved via the R package mlr which is a unified approach to machine learning with R. The below code tests all combinations of split variable numbers between two and four with forest sizes of 1 to 500 in steps of 10 and minimum node sizes of 2, 5, 8, 11 and 14.
#
# hyperparameter tuning for random forest based trading strategy
#
library("mlr")
# create task and learner
task.train <- makeClassifTask(id = "train_hl_strategy",
data = df_training,
target = "dir")
learner <- makeLearner("classif.ranger")
# set resampling strategy and search grid
res.strategy <- makeResampleDesc("CV", iters = 5)
params <- makeParamSet(makeIntegerParam("mtry", 2, 4),
makeDiscreteParam("num.trees", seq(1, 500, 10)),
makeDiscreteParam("min.node.size", seq(2, 14, 3)))
# run hyperparameter tuning
tune.res <- tuneParams(learner,
task.train,
res.strategy,
par.set = params,
control = makeTuneControlGrid())
# [Tune] Result: mtry=2; num.trees=331; min.node.size=2 : mmce.test.mean=0.2609662
# apply optimal hyperparameter set
learner.tuned <- setHyperPars(makeLearner("classif.ranger"),
par.vals = tune.res$x)
train.res <- train(learner.tuned,
task.train)
# print final results
print(train.res)
# predict on test data
df_test$dir <- as.factor(rep(0, nrow(df_test)))
task.test <- makeClassifTask(id = "test_hl_strategy",
data = df_test,
target = "dir")
predict.res <- predict(train.res, task.test)$data$response
# plot test performance of strategy
signals.test <- class_to_signal(as.numeric(as.vector(predict.res)))
performance.test <- eval_performance(v_close_test, signals.test)
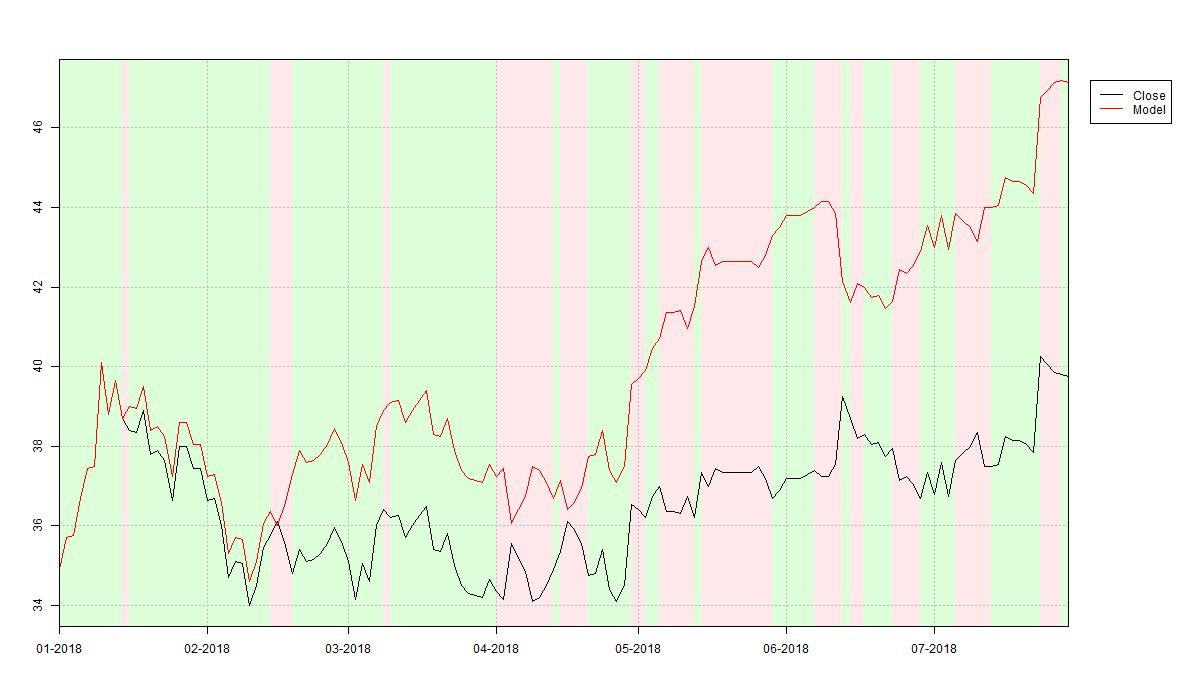
plotIndicator(v_date_test,
signals.test,
data.frame(close = v_close_test,
model = performance.test),
c("black", "red"),
c("Close", "Model"),
paste0(s_output_dir, "/HL_RandomForest_", da_cur_date, "_test_TUNED", ".jpg"))
As a result the tuned random forest features 331 trees and allows for two variables for each split with a minimum node size of 2. The trading strategy’s resulting ouf-of-sample performance is plotted below. Comparing the tuned performance to the out-of-the-box fitted strategy’s performance (see previous article) we find that the generalisation error slightly improved to 26.1%. Note that an improved generalisation error does not necessarily lead to a better out-of-sample trading performance. This is because the random forest learned to predict the direction of future price movements without providing any insights in how large the actual price move is. Misclassifying a few major price movements can thus result in a weak performance despite correctly classifying the majority of movements.
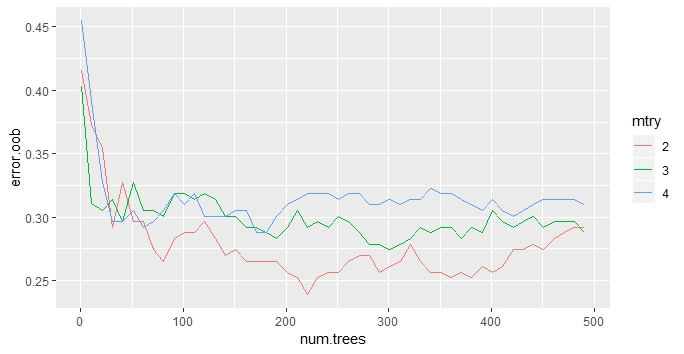
In order to understand how the mlr package performs hyperparameter tuning the below script learns a random forest manually for each of the above mentioned hyperparameter combinations without tuning “minimum node size”. For each such run the forest’s out-of-bag (OOB) error is stored and finally plotted, c.f. below. Then, for each of the three numbers of split features (mtry) the OOB error is plotted against an increasing number of trees (num.trees). The OOB error decreases quickly when increasing the number of trees for fixed mtry in the respective forest and thereafter slowly increases again. Thus, the overall optimal forest with respect to OOB error can be obtained upon determining the minimal OOB error for each path (num.trees \( \rightarrow \) error.oob), which is again two variables for the splitting but 221 trees in the forest.
Note that the result obtained by this method may vary from mlr’s result as that implementation used cross-validated generalisation error instead of OOB error: As always, one generates optimal results with respect to the selected target metric.
#
# custom hyperparameter tuning for random forest based trading strategy
#
# hyperparameter ranges
mtry <- c(2, 3, 4)
trees.nb <- seq(1, 500, 10)
# error result containers
error.oob <- matrix(rep(0, length(mtry)*length(trees.nb)),
ncol = length(mtry))
# model evaluation for each combination of hyperparameters
for (i in seq_along(mtry)) {
for (j in seq_along(trees.nb)) {
print(paste0("mtry=", mtry[i], ", num.trees=", trees.nb[j]))
model <- ranger(dir ~ .,
data = df_training,
seed = 99,
mtry = mtry[i],
num.trees = trees.nb[j])
error.oob[j, i] <- model$prediction.error
}
}
# plot in- and out-of-bag errors
error.data <- data.frame(
num.trees = rep(trees.nb, length(mtry)),
mtry = factor(rep(mtry, each=length(trees.nb))),
error.oob = c(error.oob)
)
ggplot(error.data, aes(x=num.trees, y=error.oob, group=mtry, colour=mtry)) +
geom_line()